I downloaded my facebook data and all I learned is that I have sent enough messages through their platform to enough friends to compute a power law distribution. Also, several apps sell your app-opening information to Facebook.
Introduction
I have been on Facebook since early 2005, and have uploaded quite a bit of media into the platform, although I don’t much interact with much besides using it to connect with friends and share images. The dump size on me is nearly 6GB, mostly from shared cell phone photos, images, and gifs.
Messages
My Facebook data contains 381897 messages. The message log seems to be eternal. The oldest message is from Mar 4, 2006. Some reason this predates the 2008 release of Facebook Chat significantly, or maybe that was of a different precursor to the modern Facebook messenger.
The number of messages is unsurprisingly to me heavily skewed towards a few users I message regularly, although the counts are higher than anticipated.
Will it Power Law?
With ranking users by messages as so,
| Rank | Messages | LogRank | LogMessages |
|---|---|---|---|
| 1 | 116893 | 0 | 5.067788505 |
| 2 | 63762 | 0.301029996 | 4.804561931 |
| 3 | 35812 | 0.477121255 | 4.554028576 |
| 4 | 25942 | 0.602059991 | 4.414003455 |
we can plot and fit a line to the rank and frequency distribution. These rank-frequency distributions often are referred to as Zipf’s law after his observations that the frequency of words used in language are inversely proportional to their rank. Other examples such as country size and population are used in the wiki article on such.
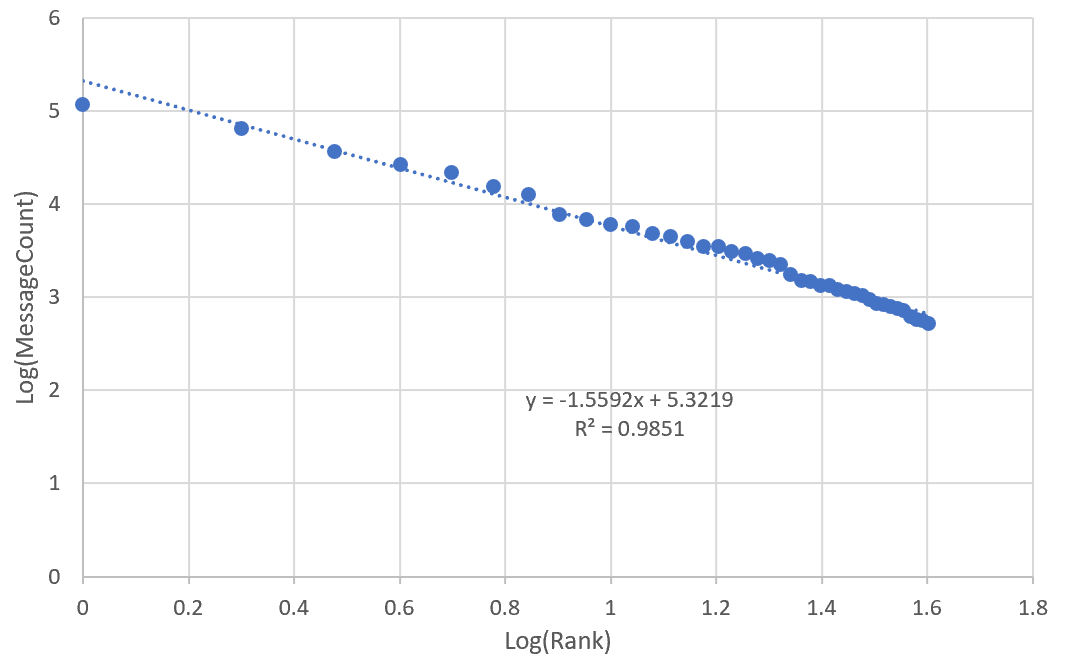
I know some will groan from the Excel chart, so I’m leaving it here.
For the sticklers who also groan about going straight to log-log plots without checking exponential or lognormal, I’ve run the data into powerlaw python package, described in this paper to fit the curve. This package allows for likelihood testing of different fits, and plot them. This package computes the log log plot of the complementary comulative distribution function, a standard method of comparison used frequently to describe rank-frequency distributions and does a decent job of logarithmically binning the data before doing fits.
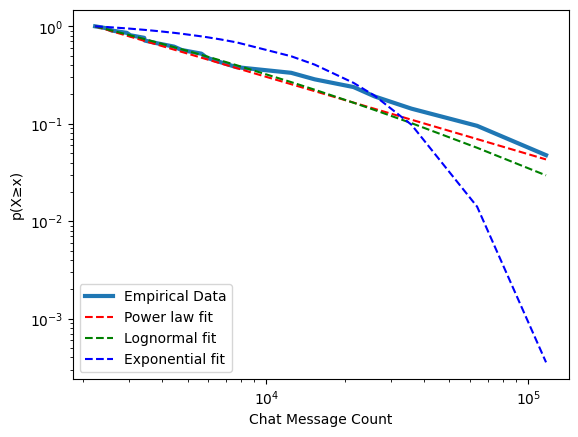
Here we can see that lognormal distribution also fits well, although the likelihood testing between it and the power law is still marginally in the favor of the power law. We also can compute the scaling coefficients, giving the probability for message count $x$ as $P(x) \propto x^{-1.8} $. Powerlaw!
Miscellaneous other remarks
Incase I don’t make a post about other items Facebook gathers…
- Photos and videos sent in messages are not eternal as messages and only seem to live a few years
- Car Dealerships are very active at paying to advertise to me
- Contains effectively a backup of my cell phone contacts
- Off-Facebook activity on me has 1356 entries, mostly page views for past few years
- Several phone apps sell your app opening information to Facebook, including:
- Airbnb
- Glympse
- One Bus Away
- Amazon Kindle
- Either has stopped, or is Android only not iOS.
Commands used to get numbers for post
I probably could have loaded the json files with some nice scripts, but chose to mostly cobble together some shell scripts to parse over things. Most should stop reading here unless you want to replicate this work on your own data.
Message Count
From the messages folder,
grep -r "timestamp_ms" | wc -l
This matches lines in subfiles that contain the word timestamp_ms, and of course there are only 1 timestamp per message.
Eldest message
From the messages folder,
date -ud @$(grep -r --no-filename "timestamp_ms" | cut -c 23-32 | sort | head -n 1)
For me this gives Sat Mar 4 20:05:33 UTC 2006.
Message counts by person
From the messages folder,
res=$(for dir in ./*; do
echo $(grep -r "timestamp_ms" $dir | wc -l) messages in $dir
done)
echo $res | sort -n -k 1 --reverse | head -n 40
Powerlaw Graph
This script. It is essentially the example given for the python package itself applied to the data.
Apps selling timestamps of you opening their App
Find and read your_off-facebook_activity.json, look for "type": "ACTIVATE_APP".